Most non-fledgling car enthusiasts will think this article is boring, but it’s a nice explainer using high-schools physics.
I’m bummed I can’t read it without a subscription. I don’t think I’ve even read any Wired articles, not sure why it says I’m all out of free articles
People with fast street cars like to put them through their paces at the quarter-mile track. One way to get your quarter-mile time is to just buckle up and put the pedal to the metal. But if your car’s design is suboptimal, you won’t be taking home the bragging rights.
So here’s this week’s question: Can automotive engineers predict a car’s quarter-mile time using physics? And could the physics suggest some tricks to make a car faster? Yes and yes! Let’s see how.
When a car launches off the start, its increase in speed is described by its acceleration (the rate of change of velocity). But according to Newton’s second law, to increase velocity, you need a force pushing in the direction of travel.
We can model the motion of a car with just three forces. There’s the downward-pulling gravitational force (= mass, m, times the gravitational field, g). There is also the interaction between the car and the road. It’s useful to split this into two forces: One, perpendicular to the ground, is called the “normal force” (FN). It’s the resistance of the ground to gravity—what keeps a car from plunging to the center of the Earth. The other force, friction (Ff), acts parallel to the ground. Here’s a picture:
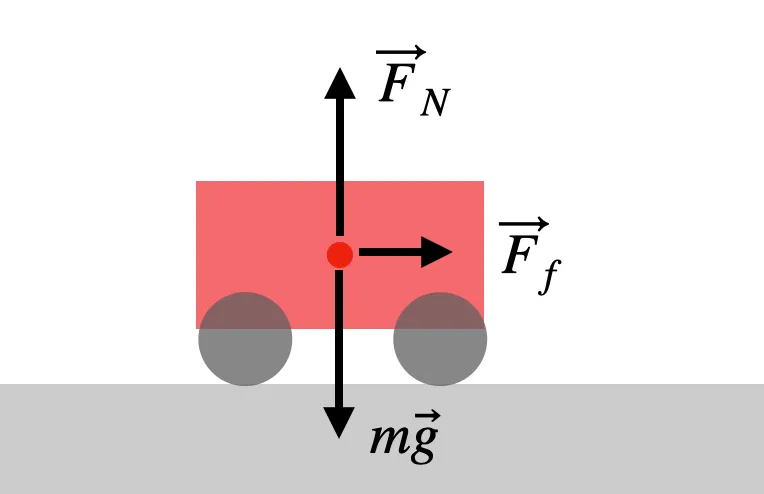
It’s the forward-pushing frictional force that makes the car accelerate. (Yes, this is powered by the engine, but the force is exerted where the rubber hits the road.) This frictional force depends on two things: the types of surfaces interacting, captured by a friction coefficient, μ, and the normal force (FN) pushing these surfaces together. With that, we get the following maximum frictional force:
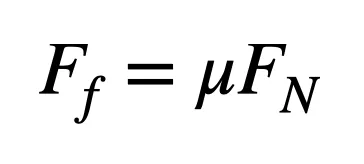
The frictional force that drives the car ahead depends on the specific materials in contact (captured by a friction coefficient, μ) and the normal force. We can quantify this by looking up the friction coefficient (around 0.7 for tires and asphalt) and calculating the normal force. Since the car stays on the ground, the acceleration in the vertical direction is zero. This means the net force in the vertical direction must be zero. So the normal force and the gravitational force must be equal.
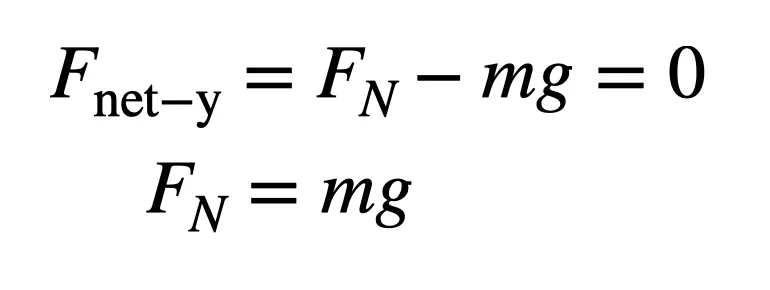
This gives us a value for the maximum frictional force (Ff). Since this is the only force in the horizontal direction, Newton’s second law says it must equal the product of the car’s mass (m) and its acceleration (a).
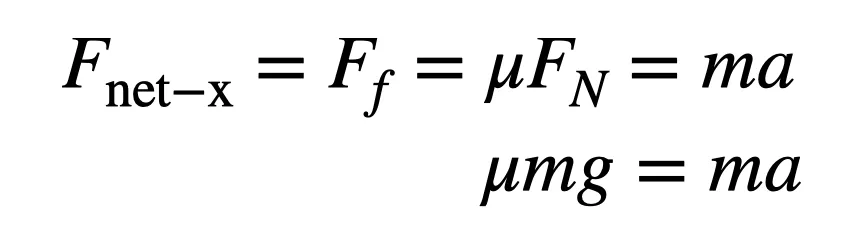
So if we know the mass of the car (m) and the coefficient of friction (μ), we can calculate the acceleration. This is going to be useful. First, however, there’s another factor we have to look at—engine power.
Constant-Power Model
Suppose you have a nice sports car. It’s red and has a nice sound system, but most importantly it’s a Porsche 911 Carrera with a 379-horsepower engine. We can use this power figure to model the motion of a car on the track. Power is something everyone thinks they understand, but most people can’t define it. So here you go: Power is the rate of change in energy.
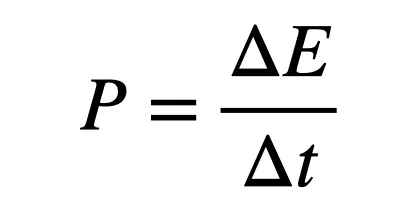
A car has kinetic energy (K) by virtue of its being in motion. The amount of kinetic energy depends on the mass of the car and its velocity (v).
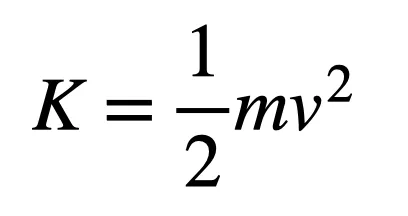
Let’s say we have a tiny car with a power of 100 watts (1 horsepower = 735 watts). If this car starts from rest, after one second it’ll have a kinetic energy of 100 joules (since 1 watt = 1 joule per second). If the car has a mass of 2 kilograms, that would give it a velocity of 10 meters per second after one second. If you double the mass (to 4 kg), it would be 7.1 meters per second.
What happens to the velocity of the 2-kg car during the next second if we assume the power is constant? It will again increase in kinetic energy by an amount of 100 joules. However, since it started at 10 m/s and this starting velocity is squared, its new velocity will be 14.1 m/s (an increase of only 4.1 m/s) at the two-second mark. And so on. With constant power, the gain in speed with each successive second gets smaller. That’s how power works.
If we apply this idea to a real car (I’m sticking with the Porsche 911), we can see how long it would take to run the quarter-mile track. I’m going to convert the power to watts and the distance to meters—it’s just easier that way. The Porsche’s mass is 1,493 kilograms (3,291 pounds), which gives me the following plot of velocity vs. time. As you can see, at 10 seconds the 911 is going 63 m/s (140 mph).
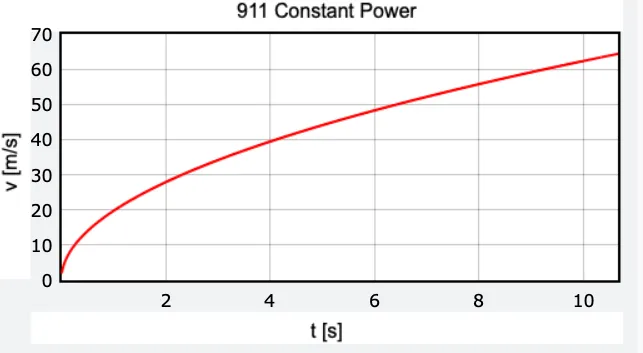
This constant-power model looks nice. It shows that the car increases in speed but not to infinity and beyond. As it goes faster, it’s acceleration (the slope of the velocity curve) decreases. Seems real.
Not so fast! There’s a problem with this model: At the start of the race, the slope of the curve is essentially vertical. That means it would have an infinite acceleration. That’s just not possible. Looking back at our equation for acceleration based on friction, the highest acceleration would be:
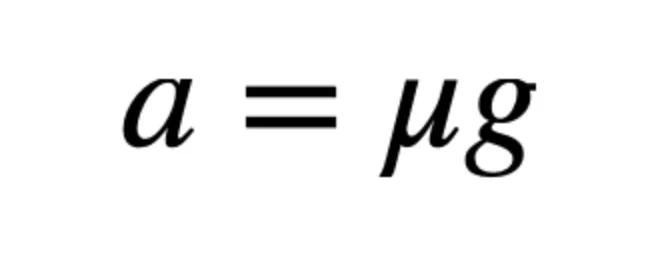
You can see that it’s limited by the materials in the tires and track (captured by the frictional coefficent) and the gravitational field (so, what planet you’re on). Notice that the mass has canceled out. It doesn’t matter if you have a more massive vehicle. Yes, you get more friction, but it’s also harder to accelerate.
Constant-Friction Model
Since constant power doesn’t work, what about a constant acceleration due to the friction between the tires and road? Let’s say the coefficient of friction is 0.7 (reasonable for a dry road). In that case we would get the following plot of velocity versus time for the quarter-mile run.
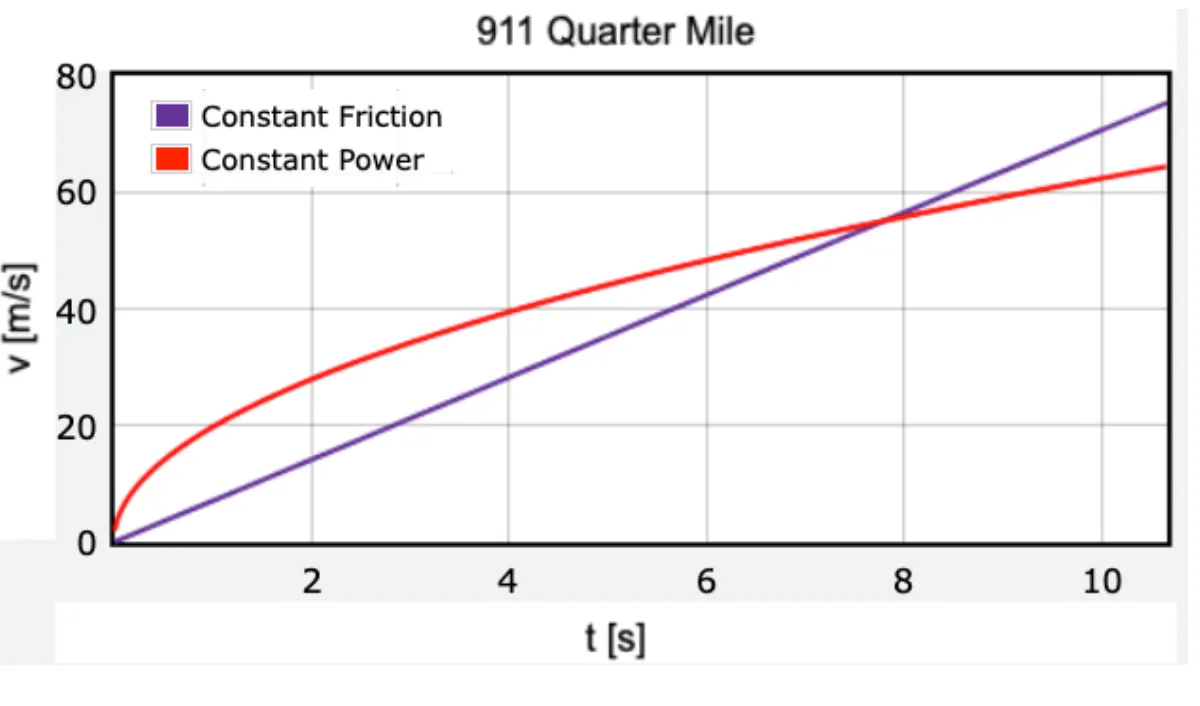
I’ve included the constant-power curve just for comparison. You can see that with this friction model, the car will just keep increasing in speed forever with the same acceleration. That doesn’t seem correct either.
A Better Model of Acceleration
How about this? The car increases in velocity—however, the rate of increase (the acceleration) is the lower of the two models. So, at the beginning of the run the acceleration is limited by the friction between the tires and road. Then, when the acceleration using the constant power model is lower, we can use that method.
Before we test this out, we need some real data for comparison. Since I don’t own a Porsche 911, I’m going to use the data from this MotorTrend race between a 911 and a Tesla Cybertruck. Here is a plot of the actual position of the Porsche over the quarter-mile track along with the combo power-friction model. (That’s now distance on the vertical axis—a quarter-mile is just about 400 meters.)
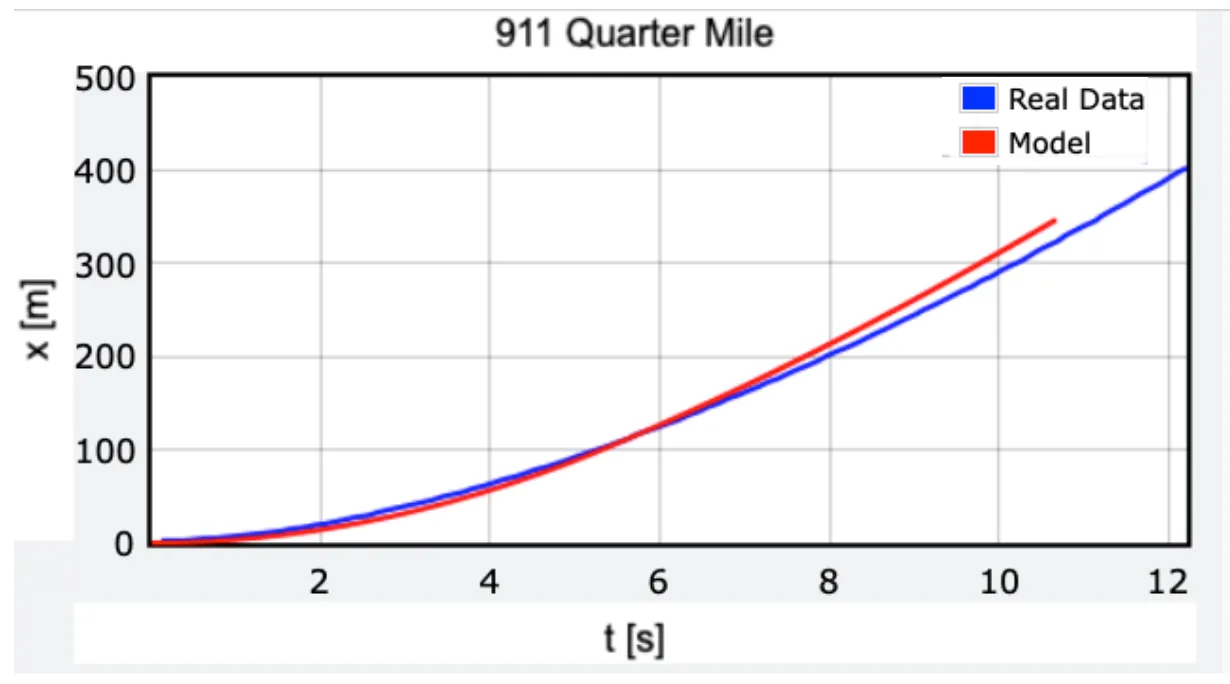
It’s not a perfect fit, but it could be. I lowered the power of the Porsche a bit in my model because not all of those 379 horses go into the kinetic energy of the car—it’s not a perfectly efficient system. But still, this fairly powerful car hits a quarter-mile in 12.2 seconds with a final speed of 116.4 mph (from MotorTrend). Is it possible to get a lower time? Yes. With physics.
Cheating With Physics
The dilemma is that our car is limited by the frictional force at the start. You can raise the coefficient with drag-car tires, but you won’t be driving home on those. Alternatively, you can boost the friction by increasing the mass of a car. But then you also have more mass that needs to accelerate, so you don’t gain anything. The key is to increase the frictional force without increasing the mass.
Now, there are “super cars” that can do the quarter mile in a crazy 10 seconds. (The sticker prices are crazy too.) But forget that. What if I told you there’s a road-legal “hypercar” that can do it in under 8 seconds? True fact. The McMurtry Spéirling clocked a time of 7.97 seconds, even on a slightly wet road. The secret? It has fans that pull air out from underneath, creating a pocket of low air pressure that sucks the car downward.
Let me just go ahead and draw a force diagram for a car with a fan.
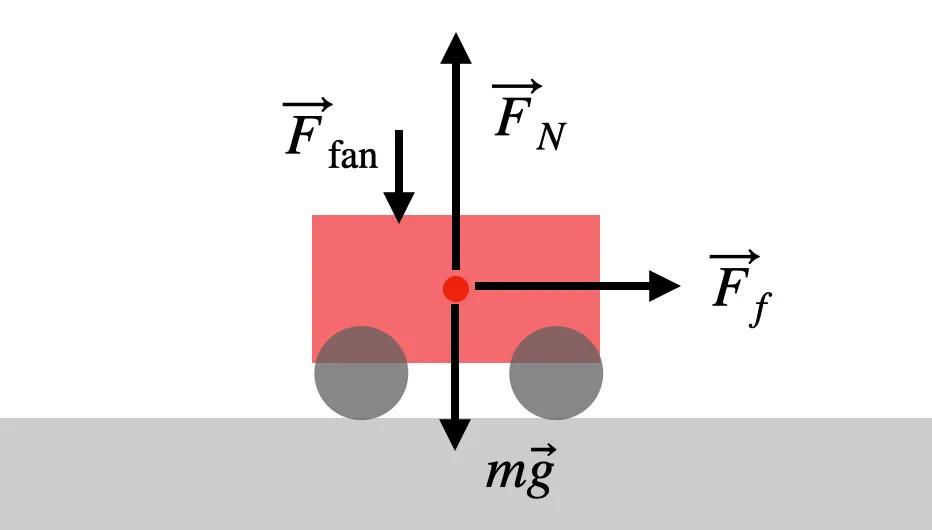
Even though there’s an extra downward pushing force (Ffan), the car stays on the ground and still has a zero acceleration in the vertical direction. In this case, Newton’s second law looks like this:
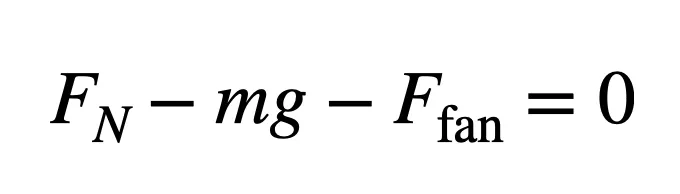
With the extra downward force, the only way for the forces to add up to zero is if the normal force increases. This means the frictional force is greater, so the new acceleration is greater.
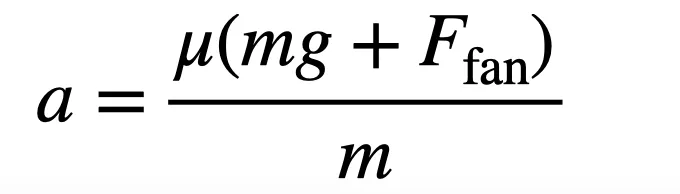
Now instead of getting a maximum acceleration of 6 to 7 meters per second squared, it’s possible to get much higher values—maybe 15 or even 20 m/s2. The McMurtry Spéirling in the video went from 0 to 60 mph in … wait for it … 1.4 seconds. Just thinking about that will pin your ears back.
The fan idea isn’t new. In 1978, the Brabham BT46B used it to win the Formula 1 Swedish Grand Prix, but it was quickly banned. The idea of increasing downward force lives on, however. F1 cars today channel airflow through the body in clever ways to achieve some of the same “ground effect”—justified by saying the purpose is to cool the engine.
While these airflow systems do help cool the engine, everyone knows the real purpose is to generate low pressure under the car to suction it closer to the road. In fact, the new McLaren W1 that we recently reviewed is a road car that bases its sales pitch on this. (You can buy one for $2.6 million—or you could have if you’d signed up in time. Only 399 are being made, and they’re all spoken for.)
The cool part is that this higher acceleration isn’t just for increasing your speed. It also allows the car to slow down faster and even make sharper turns, since these are also types of acceleration. The downward thrust can turn a fast car into a crazy-fast car—if that’s what you want. For me, I’m happy as long as it’s a red car and it drives.
Rhett Allain is an associate professor of physics at Southeastern Louisiana University. He enjoys teaching and talking about physics. Sometimes he takes things apart and can’t put them back together.
There you go, bud!
Lmao that was a lot more scrolling than I expected when I saw the “there you go bud” notification, thank you so much man I appreciate it
Hope you have a good one!
You betcha, friend! Take it sleazy.
Lol, thank you friend, I will!
Fun fact: robot mice competitions use fans to suck air under the mice to increase grip enough for the high speed maneuvers.
Look up videos of the competitions, it’s mind blowing.



